เคยไหมเวลาแฮงค์เอาต์แล้วต้องหารค่ารถกับเพื่อนที่บ้านอยู่ทางเดียวกัน แต่ดันไม่รู้ว่าจะหารยังไงถึงจะเรียกว่าแฟร์กับทุกคนที่สุด?
เรื่องทั้งหมดนี้มักเกิดขึ้นหลักปาร์ตี้ ที่สมาชิกปาร์ตี้สามคนต้องหาวิธีการกลับบ้าน ในเวลานั้นการโบกแท็กซี่ดูจะเป็นทางเลือกเดียว และด้วยความที่ปลายทางของทั้งสามคนอยู่ในทิศทางเดียวกัน การนั่งแท็กซี่ไปด้วยกันแล้วแวะส่งทีละคนจึงดูจะเป็นตัวเลือกที่ดีที่สุด คำถามคือแล้วทั้งสามคนจะหารค่าแท็กซี่กันอย่างไรดีให้ยุติธรรมที่สุด คือแค่หารค่าแท็กซี่น่ะมันไม่ได้ยากในตัวมันเองหรอก จุดที่ยากคือต้องให้ยุติธรรมนี่สิ
เพื่อให้คุยกันง่าย เราสมมติว่าคนสามคนนั้นชื่อว่า A B และ C เรียงตามลำดับการลงรถ โดยราคาบนมิเตอร์ ณ จุดที่แต่ละคนลงเท่ากับ 60 80 และ 200 บาทตามลำดับ
วิธีที่ง่ายที่สุดเพื่อตัดปัญหาก็คือเอา 200 หารด้วย 3 จบ แต่ A น่าจะไม่จบ เพราะ A จะวีนว่าฉันนั่งใกล้ที่สุดแล้วทำไมฉันต้องจ่ายเท่าคนอื่นด้วย เงินที่จ่ายก็ควรจะแปรผันกับระยะทางที่นั่งไปสิ จึงนำมาสู่วิธีที่สองที่คิดว่าหลายคนน่าจะใช้กันก็คือ เอาราคาแต่ละช่วงมาหารแจกให้คนบนรถตอนนั้น อย่างในกรณีของเรา 60 บาทแรกจะถูกหารจ่ายโดยคนสามคน คนละ 20 บาท 20 บาทต่อมา (คือช่วงหลัง A ลงจนถึงจุดที่ B ลง) ก็เอาไปหารแจกเฉพาะ B กับ C คนละ 10 บาท และช่วง 120 บาทสุดท้าย C ก็จ่ายไปเต็มๆ (ตามภาพ)
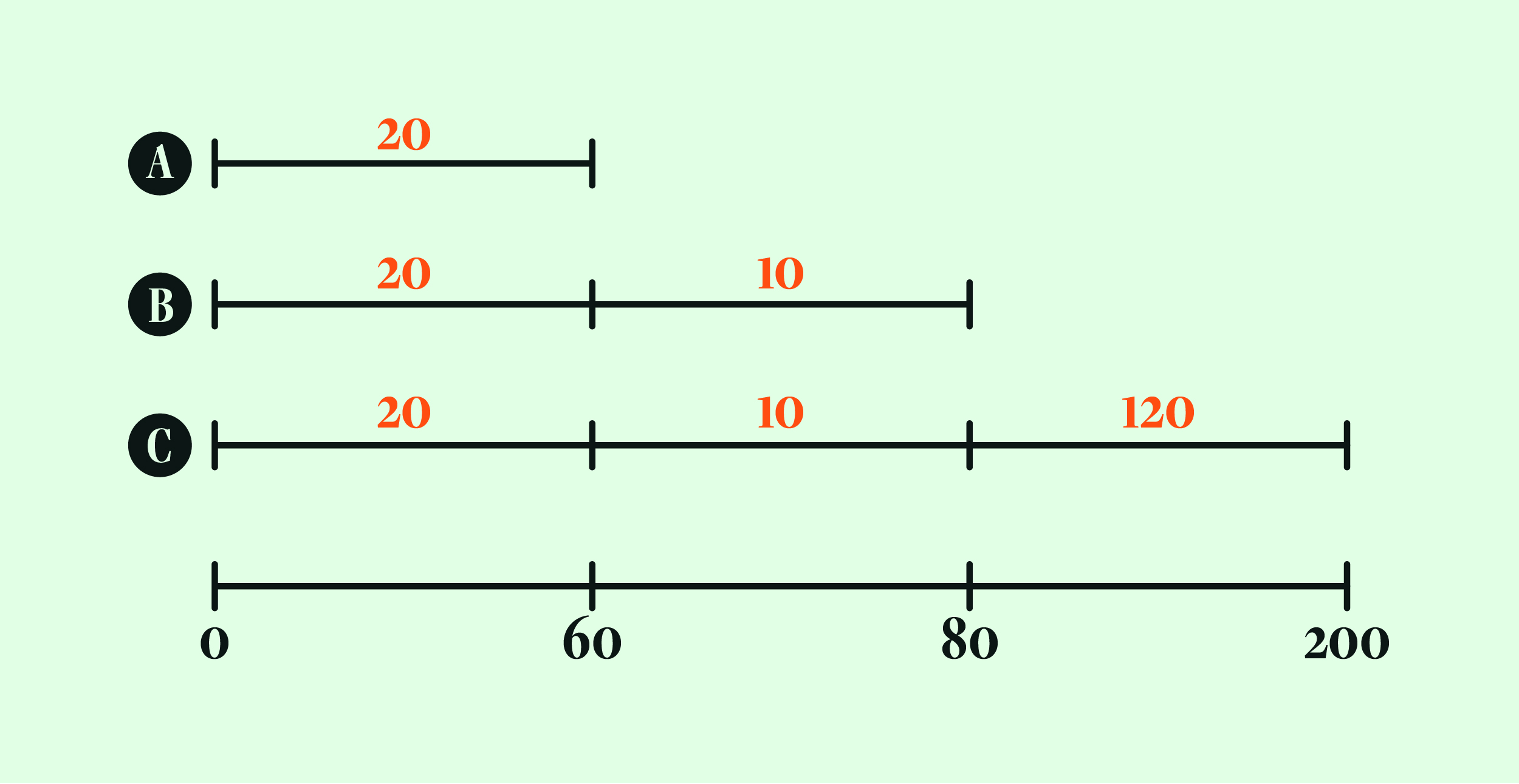
ด้วยวิธีคิดแบบนี้จะทำให้ A จ่าย 20 บาท B จ่าย 30 บาท และ C จ่าย 150 บาท ฟังดูดี คิดเลขง่าย ดูแฟร์ และทุกคนน่าจะแฮปปี้ แต่เมื่อลองคิดดูให้ดีจะพบว่า ลองไปคำนวณส่วนที่แต่ละคนประหยัดไปจะเท่ากับ66.67% 62.5% และ 25% ตามลำดับ ซึ่งไม่เท่ากัน และกลายเป็นว่า C จะได้ประโยชน์จากการแชร์รถครั้งนี้น้อยกว่าใครเพื่อน
ยิ่งไปกว่านั้น ถ้าจุด A B C นั้นไม่ได้เรียงกันเป็นเส้นตรงล่ะ ถ้าเกิดว่าจริงๆ แล้วร้านไปปลายทางของ C มันควรจะราคาแค่ 170 บาท แต่ที่มันกลายเป็น 200 บาทนั้นเพราะว่าต้องอ้อมไปส่ง A กับ B ล่ะ ดังนั้น A กับ B ก็ควรจะต้องมีส่วนร่วมใน 120 บาทในช่วงสุดท้ายด้วยในฐานะคนทำให้อ้อมหรือเปล่า
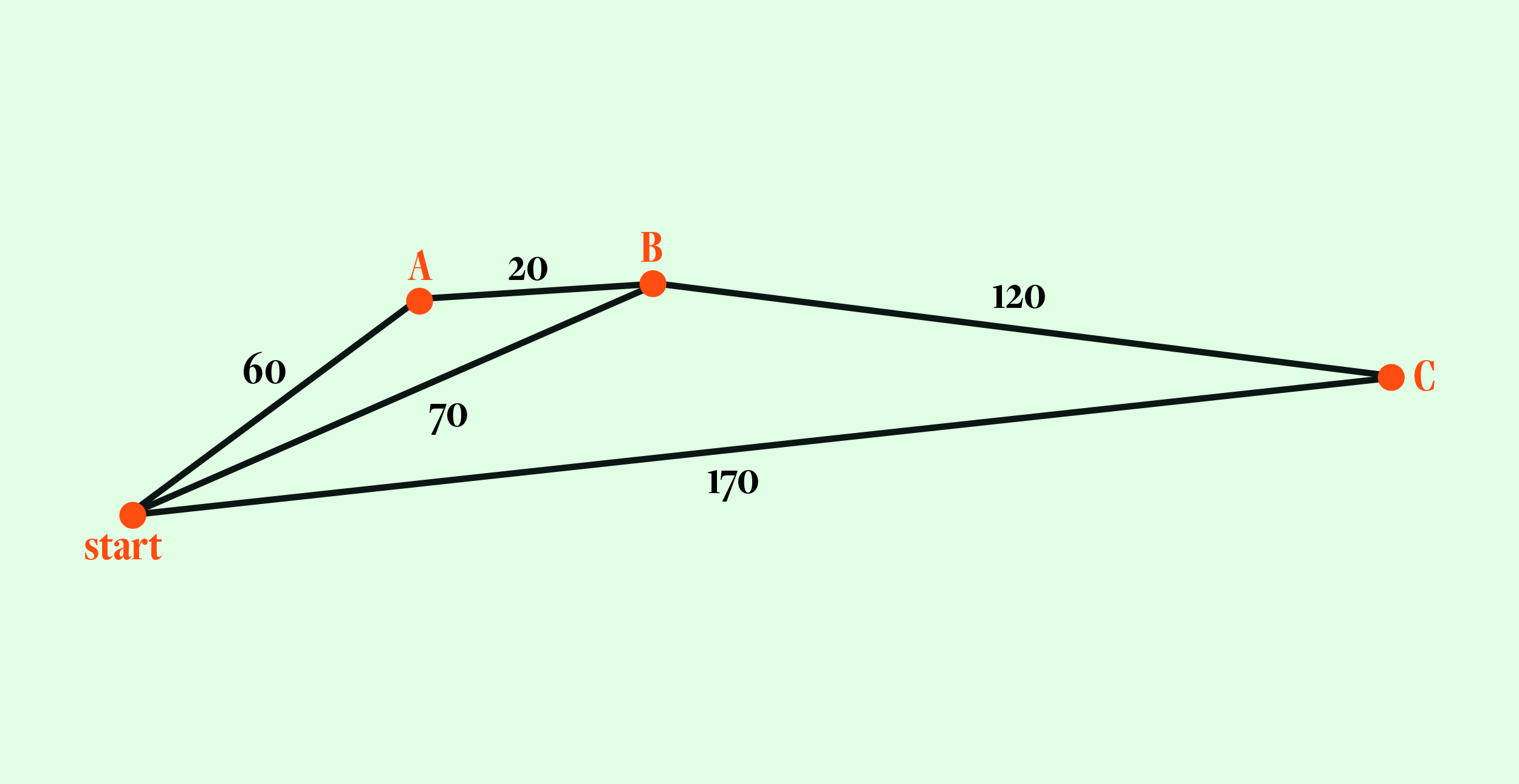
จึงเกิดเป็นวิธีที่สามขึ้นมา วิธีนี้ซับซ้อนหน่อย เริ่มจากการเอาค่าโดยสารที่แต่ละคนต้องจ่ายในกรณีที่ต่างคนต่างกลับมารวมกัน อย่างในรูปนี้จะเห็นว่าคือ 60 70 และ 170 บาทตามลำดับ รวมเป็น 300 บาท ดูว่าส่วนของแต่ละคนคิดเป็นสัดส่วนของเงินก้อนนี้ ได้ 20% 23.33% และ 56.67% ตามลำดับ แล้วเอาเปอร์เซ็นต์พวกนี้ไปหาสัดส่วนของเงินที่ต้องจ่ายจากราคา 200 บาท นั่นคือสุดท้ายแล้วแต่ละคนต้องจ่าย 40 บาท 46.66 บาท และ 113.34 บาทตามลำดับ
การคิดเป็นอัตราส่วนแบบนี้อาจจะแฟร์ขึ้นในมุมที่ว่าอัตราส่วนของเงินที่ทุกคนต้องจ่ายเมื่อเทียบกับคนอื่นนั้นยังเท่ากับการต่างคนต่างนั่งกลับบ้าน แค่ทุกคนได้จ่ายในราคาถูกลงไปด้วยกัน น่าจะเป็นวิธีที่แฟร์ที่สุด แต่กลายเป็นวิธีที่ทำได้ยากในทางปฏิบัติ
เพราะการจะคำนวณด้วยวิธีอัตราส่วนนี้ได้อย่างแม่นยำนั้น แต่ละคนต้องรู้ว่าถ้าตัวเองนั่งแท็กซี่ตรงไปปลายทางของใครของมันเลยนั้นจะราคาเท่าไร ซึ่งเป็นค่าที่ไม่มีใครรู้ทำได้แค่ประมาณเอาเท่านั้น สิ่งที่พอทำได้ก็จะเป็นแค่การเอา 60 80 และ 200 มาบวกกันตรงๆ เป็น 340 แล้วก็ไปคิดอัตราส่วนของแต่ละคนจาก 340 แทน ซึ่งได้ผลลัพท์ออกมาเป็น 35.29 47.06 และ117.65 บาท ผลลัพท์นี้ดูไม่ต่างจากการคิดจากเงินรวม 300 เท่าไรนัก เนื่องจากการแวะไปส่ง A กับ B ไม่ได้ทำให้อ้อมมาก เพราะถ้าต้องอ้อมกว่านี้สักหน่อย การประมาณแบบนี้ก็จะทำให้ C เสียเปรียบได้

แต่ทั้งหมดนี้คือสถานการณ์แบบโลกสวย ทุกคนเป็นเพื่อนกันอยากให้ทุกอย่างแฟร์เพื่อมิตรภาพที่ยืนยาว แต่ลองนึกภาพว่าถ้าสถานการณ์นี้เกิดขึ้นกับคนสามคนที่ไม่ได้รู้จักกันมาก่อน แค่บังเอิญเจอกันและพยายามจะดีลกันเท่านั้น และอาจจะล่มดีลทิ้งเมื่อไรก็ได้เมื่อตกลงผลประโยชน์ไม่ลงตัว ดังนั้นแม้จะเป็นการพยายามดีลกันให้แฟร์ที่สุดเหมือนเดิม แต่คำว่าแฟร์ในที่นี้จะไม่เหมือนเดิมอีกต่อไป
ในวิชาทฤษฎีเกมมีปัญหาอยู่ข้อหนึ่งที่เรียกว่าปัญหาการต่อรอง (Bargaining Problem) ที่ผู้เล่นแต่ละคนจะพยายามต่อรองกันเพื่อให้ตนได้ผลประโยชน์สูงที่สุด ตัวอย่างง่ายที่สุดของปัญหาการต่อรองคือการต่อรองราคา เกมนี้มีผู้เล่นอยู่สองคนคือผู้ซื้อกับผู้ขาย ทั้งคู่ต้องตกลงราคาสินค้าชนิดหนึ่งกัน สมมติว่าราคาสูงสุดที่ผู้ซื้อจะจ่ายไหวคือ 1,000 บาท และราคาต่ำที่สุดที่ผู้ขายจะขายไหวแบบไม่ขาดทุนคือ 600 บาท
และถ้าทั้งคู่รู้ตัวเลขในใจของอีกฝ่าย สถานการณ์ที่ดีที่สุดที่เกิดขึ้นได้คือขายที่ราคา 800 บาทซึ่งเป็นการพบกันครึ่งทาง ผู้ซื้อก็จะมีความสุขที่ได้ซื้อถูกกว่าราคาในใจไปตั้ง 200 บาท เท่ากับที่ผู้ขายจะมีความสุขจากการขายได้สูงกว่าราคาในใจ ราคา 800 บาท สิ่งนี้เรียกว่า ผลลัพธ์การต่อรองของแนช (Nash Bargaining Solution) ที่ตั้งชื่อตามจอห์น ฟอบส์ แนช (John F. Nash) ซึ่งเป็นบิดาของวิชาทฤษฎีเกม หลักคิดของเขาก็คือมองว่าสถานการณ์ตอนนี้มีผลประโยชน์ส่วนเกิน (surplus) อยู่ 400 บาท ซึ่งคิดมาจากกำไรที่ผู้ขายจะได้ถ้าตั้งราคาไว้แพงที่สุด หรือส่วนลดที่ผู้ซื้อจะได้ถ้าตั้งราคาขายไว้ต่ำที่สุด จอห์นเสนอว่าผลลัพธ์ที่ดีที่สุดของสถานการณ์นี้คือการเอาผลประโยชน์ส่วนเกินมาแบ่งให้ผู้เล่นทุกคนเท่าๆ กัน

กลับไปที่ปัญหารถแท็กซี่ ผลประโยชน์ส่วนเกินในสถานการณ์นี้คือ 100 บาท ซึ่งคิดมาจากผลรวมของค่าโดยสารหากแต่ละคนไปรถคนละคัน 300 ลบด้วยราคารวมที่ต้องจ่ายจริงซึ่งคือ 200 ถ้าคิดด้วยวิธีของแนชจะได้ว่าผลประโยชน์ส่วนเกินนี้จะต้องถูกหารแบ่งให้แต่ละคนคนละ 33.33 บาท ซึ่งแปลว่าทุกคนจะได้ส่วนลดค่าเดินทางจากการแชร์รถครั้งนี้เป็นจำนวนเงินเท่าๆ กัน ไม่ใช่คิดตามอัตราส่วนเหมือนในวิธีก่อนๆ
แต่ถ้าสถานการณ์เปลี่ยนไปนิดหน่อยกลายเป็นว่า A กับ B นั้นรวมหัวกันได้สำเร็จแล้วบอก C ว่า พวกฉันสองคนพร้อมจะไปกันเองแล้วจ่ายแค่แพงขึ้นนิดโดยไม่มีแกก็ได้ ดังนั้นถ้าแกอยากจะเข้ามาจอยรถกับเราด้วย เธอก็ต้องยอมจ่ายแพงกว่านะ คราวนี้วิธีการคำนวณผลประโยชน์ส่วนเกินจะเปลี่ยนไป และส่วนแบ่งค่าแท็กซี่ก็จะเปลี่ยนไปด้วย ซึ่งก็ต้องอาศัยความรู้ทฤษฎีเกมที่ซับซ้อนขึ้นตามสถานการณ์ อีกทั้งความรู้เรื่องปัญหาการต่อรองก็สามารถนำไปประยุกต์ใช้ในโลกความเป็นจริงเยอะมาก โดยเฉพาะโลกธุรกิจ การต่อรองกันของนายจ้างและลูกจ้าง การต่อรองกันระหว่างสองบริษัท ไปจนถึงการเมืองระหว่างประเทศ รวมทั้งสถานการณ์อะไรก็ตามที่ต้องมีการประสานผลประโยชน์ระหว่างผู้มีส่วนได้ส่วนเสียหลายฝ่าย
กลับมาที่เรื่องการหารค่าแท็กซี่ สรุปแล้วเราควรใช้วิธีไหน ส่วนตัวคิดว่าถ้าเราเป็นเพื่อนกัน การหารแบ่งด้วยอัตราส่วนจึงน่าจะดูเป็นวิธีที่เข้าท่าที่สุด เพราะก็แฟร์ดี คิดเลขไม่ยาก และในทางปฏิบัติเราคงไม่อยากขึ้นแท็กซี่กับคนแปลกหน้าอยู่แล้ว การพยายามเจรจาต่อรองกันด้วยแนวคิดแบบทฤษฎีเกมกับเพื่อนคงจะไม่ดีต่อมิตรภาพในระยะยาว แต่ถ้าใครไปกับแก๊งที่อยู่กันเป็นครอบครัวแบบในเลือดข้นคนจาง หรืออยู่กันแบบพี่น้องแบบบ้านซินเดอร์เรลล่า การรู้ทฤษฎีเกมไว้บ้างก็อาจจะเป็นเรื่องจำเป็น
อ้างอิงจาก