เสน่ห์ที่ทำให้การ์ตูนจากค่าย Pixar ครองใจคนทั้งโลกได้นั้น นอกจากเนื้อเรื่องที่สนุกแล้วคืออนิเมชั่นที่น่ารักสวยงาม ตัวละครที่ดูสมจริง หน้าตา ท่าทาง และการเคลื่อนไหว สิ่งเหล่านี้แน่นอนว่าก็คงต้องให้เครดิตกับฝ่ายศิลป์ ทีมออกแบบตัวละคร ทีมอนิเมชั่น แต่น้อยคนจะรู้ว่าเบื้องหลังความสำเร็จนี้มีทีมนักคณิตศาสตร์มือเทพอยู่เบื้องหลังด้วย
โทนี่ เดอโรส (Tony DeRose) หัวหน้าทีมวิจัยของ Pixar เคยพูดใน TedTalk ของเขาว่า “คณิตศาสตร์ที่พวกเราเรียนกันในมัธยมต้นและมัธยมปลายนั้นถูกใช้อยู่ตลอดเวลาใน Pixar”
ตัวอย่างที่โทนี่ยกประจำไม่ว่าเขาจะไปพูดที่ไหนคือเรื่องตัวละคร Geri หรือคุณลุงที่เล่นหมากรุกคนเดียวจากการ์ตูนสั้นเรื่อง Geri’s Game ที่ออกฉายในปี ค.ศ.1997

จะเห็นได้ว่าผิวหนังและมือของ Geri นั้นมีความเนียนสวย และเคลื่อนไหวได้อย่างสมจริง ซึ่งสิ่งนี้ถูกทำขึ้นได้ด้วยคณิตศาสตร์
ก่อนจะไปถึงตรงนั้น มีความรู้พื้นฐานบางอย่างที่ต้องทบทวนกันก่อน เริ่มต้นจากเรื่องระบบพิกัดฉาก ในคณิตศาสตร์ เวลาเราจะพูดถึงตำแหน่งของอะไรสักอย่าง เราจะใช้ตัวเลข 2 ตัว นั่นคือตำแหน่งบนแกน X ในแนวนอน และตำแหน่งบนแกน Y ในแนวตั้ง
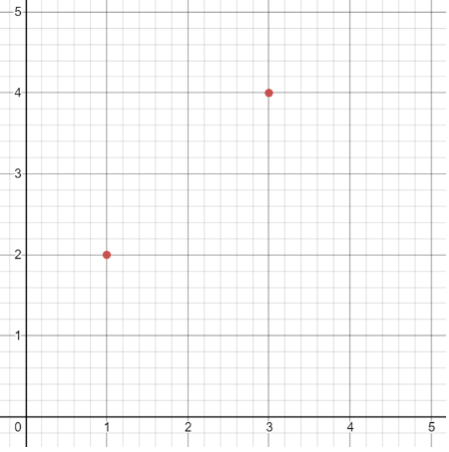
เช่นถ้าเราพูดว่า จุด (1,2) ก็หมายถึงจุดนั้นอยู่ห่างจากจุดอ้าอิงไปทางขวา 1 หน่วย และทางด้านบน 2 หน่วย หรือถ้าพูดว่าจุด (3,4) ก็จะหมายถึงที่อยู่ห่างจากจุดอ้างอิงไปทางขวา 3 หน่วย และทางด้านบน 4 หน่วย
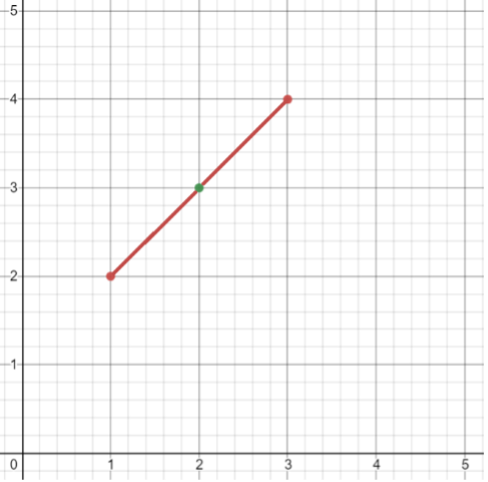
ทีนี้ถ้าเราอยากหาจุดที่อยู่กึ่งกลางระหว่างสองจุดนั้น เราก็แค่เอาค่าของแต่ละแกนมาบวกกันแล้วหารด้วย 2 หรือว่าหาค่าเฉลี่ย ซึ่งในที่นี้คือ (1+3)/2 ได้เท่ากับ 2 และ (2+4)/2 นั่นคือจุด (2,3) ซึ่งจะเห็นว่ามันอยู่ตรงกลางระหว่าง 2 จุดตอนแรกพอดี
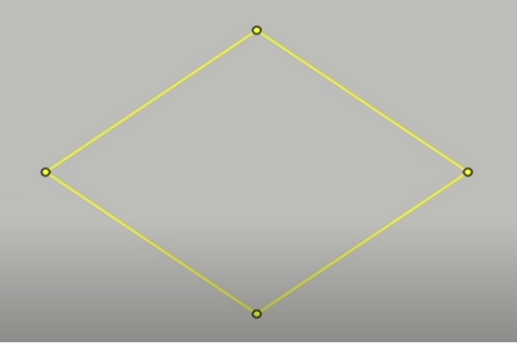
โทนี่พูดติดตลกว่า แค่เพียงความรู้เท่านี้ คุณก็สามารถทำงานที่ Pixar ได้แล้ว เราเริ่มต้นจากรูป 4 เหลี่ยมสีเหลืองที่เห็นนี้ สังเกตว่าจุด 4 จุดนั้นอยู่ห่างกันเป็นระยะเท่า ๆ กัน
จากนั้นเราหาจุดกึ่งกลางระหว่างแต่ละจุดด้วยวิธีการที่ได้อธิบายไปแล้ว คราวนี้เราจะมี 8 จุด
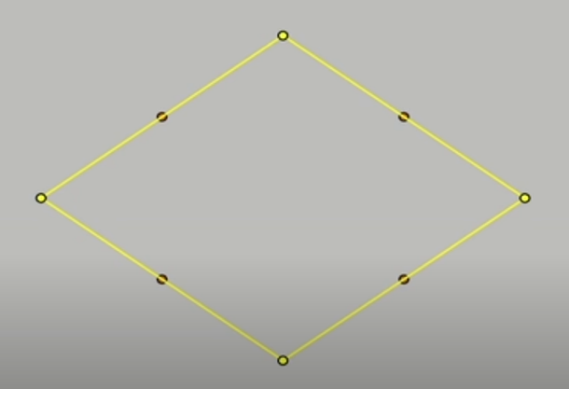
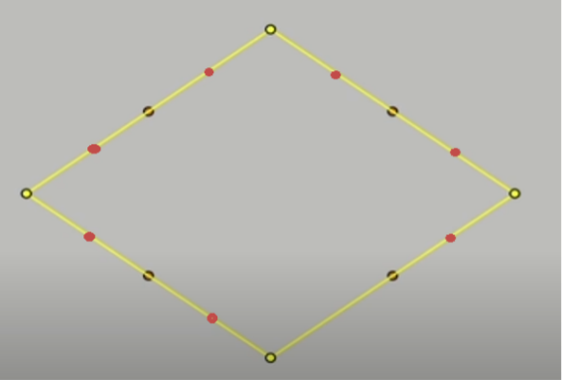
ขั้นต่อมาซับซ้อนนิดหน่อย เราหาจุดกึ่งกลางระหว่าง 8 จุดพวกนี้อีกครั้งนึง ทำสัญลักษณ์สีแดงเอาไว้ แล้วเลื่อนทั้ง 8 จุดที่เรามี หมุนตามเข็มนาฬิกาไปตำแหน่งสีแดงเมื่อสักครู่
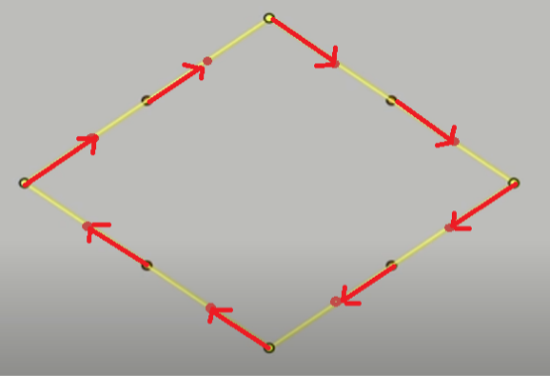
และนี่คือสิ่งที่เราจะได้
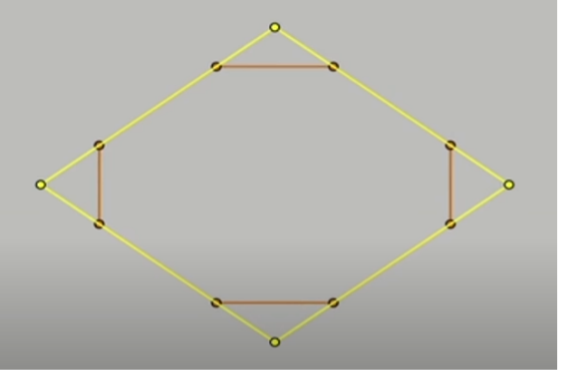
หลังจากนั้น เราแบ่งครึ่งเส้น หาจุดกึ่งกลาง เลื่อนจุด แบ่งครึ่งเส้น หาจุดกึ่งกลาง เลื่อนจุด แบบนี้วนไปเรื่อย ๆ จำนวนจุดที่เพิ่มขึ้น ก็จะทำให้รูปหลายเหลี่ยมดูเนียนขึ้น จนแทบจะกลายเป็นเส้นโค้งในที่สุด
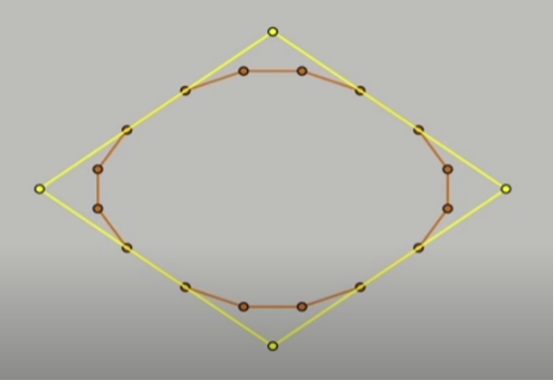
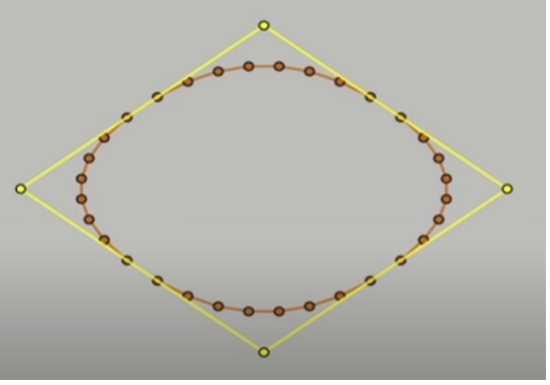
โทนี่และทีมเรียกกระบวนการสร้างเส้นโค้งจากรูปเหลี่ยมด้วยการแบ่งแล้วเลื่อนไปเรื่อยๆ แบบนี้ว่า Subdivision
อ่านมาถึงตรงนี้ หลายคนอาจจะกำลังคิดในใจว่า ถ้าอยากได้เส้นโค้งจริง ๆ ทำไมเราไม่แค่เอาปากกาลากเส้นโค้งสีน้ำตาลไปเลย จะมามัวทำขั้นตอนให้ยุ่งยากซับซ้อนแบบนี้ทำไม
คำตอบก็คือเพราะตัวละครเหล่านี้ต้องเคลื่อนไหว ในความเป็นจริงเวลาเราเห็นว่าเส้นมันเคลื่อนไหวในการ์ตูน สิ่งที่เคลื่อนไหวจริงๆ ไม่ใช่เส้น แต่คือจุด มันคือจุดที่เคลื่อนไหวไปพร้อมๆ กัน ดังนั้นถ้าเราอยากให้รูปรูปหนึ่งไปทางไหน เราก็ต้องสั่งให้จุดที่ประกอบกันเป็นเส้นพวกนั้นเคลื่อนที่ไป ยิ่งเส้นโค้งเนียนมากเท่าไร ก็แปลว่าเราต้องควบคุมจุดจำนวนมากขึ้นเท่านั้น ซึ่งไม่ใช่งานที่ง่ายเลย
แต่ความพิเศษของเส้นโค้งที่เกิดจากการทำ Subdivision ก็คือ ถ้าเราไปขยับจุด 4 จุดในสี่เหลี่ยมรูปแรก เส้นโค้งสุดท้ายที่เรามันก็จะขยับไปด้วยเอง นั่นแปลว่าเราสามารถควบคุมการเคลื่อนไหวของเส้นโค้งนั้นทั้งเส้น โดยผ่านการควบคุมแค่ 4 จุดตอนเริ่มต้นเท่านั้น ซึ่งง่ายกว่ากันมาก
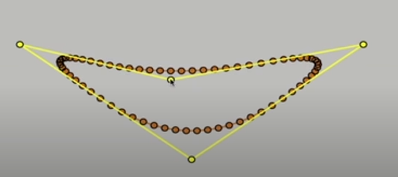
ในกรณี 3 มิติก็ทำได้เช่นกัน จากรูปเริ่มต้นที่เป็นเหลี่ยม ๆ นั้น เราสามารถทำให้มันเนียนขึ้นได้ด้วย Subdivision เพียงแค่สูตรการหาค่าเฉลี่ยอาจจะซับซ้อนขึ้นนิดหน่อย
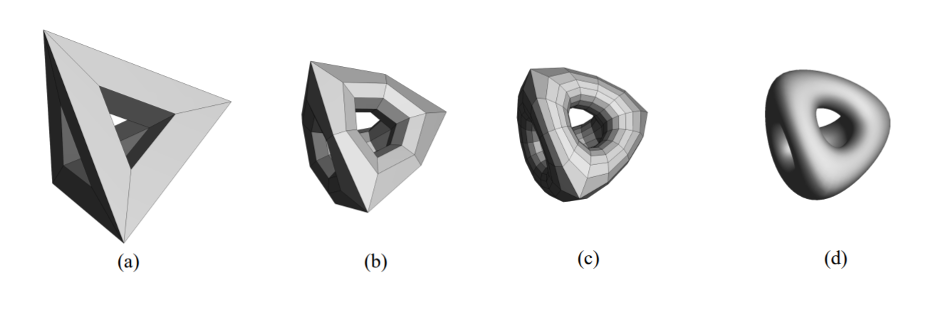
กระบวนการสร้างตัวละคร Geri นั้นเริ่มต้นด้วยการปั้นหุ่นต้นแบบขึ้นมาก่อน ใช้กล้องถ่าย และสร้างเป็น Geri แบบเหลี่ยมๆ ในคอมพิวเตอร์ หลังจากนั้นก็ไปทำ Subdivision ให้ออกมาเป็น Geri เวอร์ชั่นผิวเนียน ที่สามารถคุมควบการเคลื่อนไหวได้ผ่านการขยับของจุดไม่กี่จุดเท่านั้น


ทีมวิจัยยังไม่หยุดแค่นั้น แต่ยังศึกษาไปต่อ ถึงขั้นตอนการหาจุดกึ่งกลางว่า ถ้าเราเปลี่ยนจากจุดกึ่งกลางระหว่างสองจุด ไปเป็นจุดที่เยื้องๆ ออกไปหน่อย ผลลัพท์สุดท้ายที่ได้จะเปลี่ยนไปยังไง ซึ่งตรงนี้ต้องใช้คณิตศาสตร์ที่ซับซ้อนกว่าเดิมเข้ามาช่วย
ไม่ใช่แค่ผิวเนียนๆ ของตัวละคร แต่ทีมนักคณิตศาสตร์ของ Pixar ยังวิจัยเกี่ยวกับการสร้างสมการเพื่อความสมจริงของอนิเมชั่นอีกมากมาย อีกผลงานที่สร้างชื่อให้พวกเขาคือผมหยิกยาวสีแดงของเมริดาในเรื่อง Brave ซึ่งมีความซับซ้อนมาก ใครที่เคยดู Brave จะรู้ดีว่าเมริดาวิ่งไปวิ่งมาทั้งเรื่อง และทุกครั้งที่เธอวิ่งนั้น ผมของเธอสะบัดได้อย่างสวยงามสมจริงมาก

การสร้างผมหยิกให้ดูสมจริงนั้นนั้นยากกว่าการสร้างผมตรงมาก เพราะว่าเส้นผมที่ตรงนั้นก็จะชี้ลงพื้นตามแรงดึงดูดของโลก แต่สมการที่นักคณิตศาสตร์ใช้อธิบายการเกิดผมหยิกนั้นซับซ้อนมาก จึงเป็นงานยากของทีมงานที่ต้องสร้างผมที่หยิกด้วยคอมพิวเตอร์ ให้ออกมาดูเป็นธรรมชาติ
ไม่ใช่แค่ผิวของ Geri และผมของเมริดา แต่ทีมวิจัยของ Pixar ยังมีการใช้สมการคณิตศาสตร์เข้ามาเพื่อเพิ่มความสมใจให้กับภาพ แสง สี หรือการเคลื่อนไหวของตัวละครอยู่อย่างต่อเนื่อง เยอะจนรวบรวมเป็นคลังงานวิจัยคณิตศาสตร์ของพวกเขาเองเลย เปิดให้โหลตมาอ่านได้ฟรีด้วย ใครสนใจก็ลองเข้าไปดูได้ที่นี่เลย
https://graphics.pixar.com/library/
แน่นอนว่าทีมงานคณิตศาสตร์ของ Pixar นั้นยังไม่หยุดพัฒนาเท่านี้ เราในฐานะคนดูก็คงต้องรอติดตามกันต่อไป ว่าพวกเขาจะมีผลงานน่าตื่นเต้นอะไรให้เราได้เซอร์ไพรส์กันอีก
อ้างอิงภาพและข้อมูลจาก