ถ้าอยากหาคำตอบในเรื่องลึกลับหรือคดีฆาตกรรม ต้องใช้วิทยาศาสตร์เข้าช่วยหาคำตอบเท่านั้นหรือ?
ใครที่เป็นสาย true crime มือสมัครเล่น ชอบอ่าน ชอบฟัง เกี่ยวกับทฤษฎีสมคบคิด เรื่องลึกลับ หรือคดีฆาตกรรม น่าจะพอเคยได้ยินเรื่องราวที่วิทยาศาสตร์รับบทเป็นพระเอกในการจับคนร้ายมาบ้าง ไม่ว่าจะเป็นการสืบจากคราบรอยเลือด แนวการตัดเส้นผมที่ตกอยู่ในที่เกิดเหตุ การตรวจหารอยนิ้วมือ ไปจนถึงการวิเคราะห์ DNA เพื่อตามหาฆาตกร แต่ถ้าถามถึงคณิตศาสตร์ หลายคนอาจจะส่ายหน้า เพราะนอกจากจะไม่เคยได้ยินแล้วยังนึกไม่ออกด้วยว่าคณิตศาสตร์จะไปมีบทบาทในการไขคดีได้ยังไง
แต่มันมีอยู่ครับ บทความนี้เลยลองยกเคสที่คณิตศาสตร์ได้รับบทเป็นพระเอกมาเล่าให้ทุกคนฟังกัน
เริ่มต้นจากเคสที่ไม่ใช้คณิตศาสตร์เข้ามาช่วยตอนเกิดคดีขึ้นจริง แต่ถูกเอามาวิเคราะห์ในภายหลัง เป็นคดีของแฮโรลด์ ชิปแมน (Harold Shipman) แพทย์เวชศาสตร์ครอบครัวชาวอังกฤษ ที่ถูกตั้งข้อหาฆาตกรรมคนไข้ในการดูแลของตัวเองจำนวน 15 คนในปี 2000 แต่จากข้อสันนิษฐานของตำรวจเชื่อว่าหมอแฮโรลด์ฆ่าคนไปทั้งหมดมากกว่า 200 คน ด้วยการให้ยาระงับประสาทชนิดรุนแรงเกินขนาด
โดยหมอแฮโรลด์กระทำการฆาตกรรมอย่างอุกอาจโดยไม่มีใครสงสัยนานถึง 3 ปี จนกระทั่งในเดือนกรกฎาคมปี 1998 แองเจล่า วูดรัฟฟ์ (Angela Woodruff) ได้แจ้งความกับตำรวจเกี่ยวกับการเสียชีวิตของแม่ของเธอ ซึ่งเป็นผู้ป่วยภายใต้การดูแลของหมอแฮโรลด์ เนื่องจากพินัยกรรมของแคทลีนได้ใส่ชื่อหมอแฮโรลด์ เป็นผู้รับผลประโยชน์เพียงคนเดียวอย่างผิดปกติ หลังจากนั้นมีการพบสารมอร์ฟีนอยู่ในร่างของผู้เสียชีวิต จนทำให้แฮโรลด์ถูกจับกุมในเดือนกันยายนในที่สุด
ในปี 2004 เดวิด สปีเกลฮัลเตอร์ (David Spiegelhalter) นักวิทยาศาสตร์อาวุโสประจำ Medical Research Council (MRC) หน่วยวิจัยชีวสารสนเทศศาสตร์ มหาวิทยาลัยเคมบริดจ์ตั้งสมมติฐานว่าหากข้อมูลการรักษาทั้งหมดของหมอแฮโรลด์ถูกนำมาวิเคราะห์ทางสถิติอย่างถูกต้อง เราอาจสามารถจับกุมหมอแฮโรลด์ ได้เร็วกว่านี้ เขามองเรื่องนี้เหมือนกับการควบคุมคุณภาพสินค้า (statistical quality control) ที่จะคอยตรวจดูการทำงานของสายการผลิต และหยุดมันลงทันทีที่มีบางอย่างผิดปกติ
โดยมองว่าผลการรักษาของหมอสักคนก็เหมือนกับการผลิตสินค้า แน่นอนว่าในการรักษาคนไข้ของหมอสักคนนั้นก็สามารถมีความผิดพลาดอันจะนำไปสู่การเสียชีวิตของคนไข้ได้บ้าง แต่มันก็ต้องไม่มากเกินไปจนผิดสังเกต และจากการวิเคราะห์จำนวนผู้ป่วยที่เสียชีวิตภายใต้การดูแลของหมอแฮโรลด์ และจำนวนผู้ป่วยที่เสียชีวิตภายใต้การดูแลของของหมอคนอื่น ด้วยเครื่องมือทางสถิติที่เรียกว่า Risk-Adjusted Cumulative Sum พบว่าเราจะสามารถเริ่มเห็นสัญญาณความผิดปกติของหมอแฮโรลด์ ตั้งแต่ปี 1985 ซึ่งเท่ากับว่าในทางทฤษฎีแล้วเราอาจจะหยุดฆาตกรต่อเนื่องรายนี้ได้เร็วกว่าที่เกิดขึ้นจริง น่าเสียดายที่ในสมัยนั้นยังไม่มีการเก็บและวิเคราะห์ข้อมูลผลการรักษาของหมอแต่ละคนให้เป็นระเบียบเรียบร้อยจนสามารถหยุดฆาตกรรมต่อเนื่องครั้งนี้ไว้ได้
เคสต่อมาเกี่ยวกับ Geospatial Profiling ซึ่งคือศาสตร์ที่ว่าด้วยการใช้เครื่องมือทางสถิติเพื่อหาความสัมพันธ์ของตำแหน่งที่เกิดเหตุแต่ละครั้ง โดยในที่นี้อาจจะเป็นบ้านที่ถูกปล้นชิงทรัพย์ต่อเนื่อง หรือสถานที่เกิดเหตุฆาตกรรมต่อเนื่องก็ได้ โดยหนึ่งในเทคนิคการทำ Geospatial Profiling ที่โด่งดังมากๆ ในช่วงปลายศตวรรษที่ 20 นั้นคือ Rossmo’s formula ซึ่งคิดค้นโดยคิม รอสโม (Kim Rossmo) นักอาชญาวิทยาชาวแคนาดา
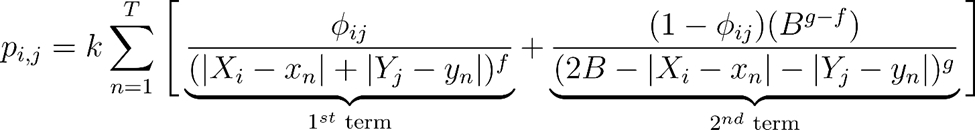
Rossmo’s formula ตั้งอยู่บนสมมติฐานที่ว่า ผู้ก่อเหตุมักจะเลือกก่อเหตุในสถานที่ที่ไม่ใกล้พักอาศัยของตัวเอง แต่ก็จะไม่ไกลจนเกินไปนัก พจน์แรกของสมการจำลองพฤติกรรมการไม่ก่อเหตุใกล้ที่พักมากเกินไป ส่วนพจน์ที่สองจำลองพฤติกรรมการก่อเหตุให้ห่างจากสถานที่ที่ตนเองอยู่ออกไปหน่อย
เมื่อเกิดคดีครั้งแรก สมการนี้จะช่วยให้เรามองเห็นได้ว่าที่พักของคนร้ายนั้นอยู่ห่างไปจากจุดเกิดเหตุประมาณเท่าไร และเมื่อเกิดคดีที่สอง สาม สี่ เราก็จะสามารถคำนวณหาความน่าจะเป็นเพื่อคาดการณ์ว่าที่พักของคนร้ายน่าจะอยู่บริเวณไหนกันแน่
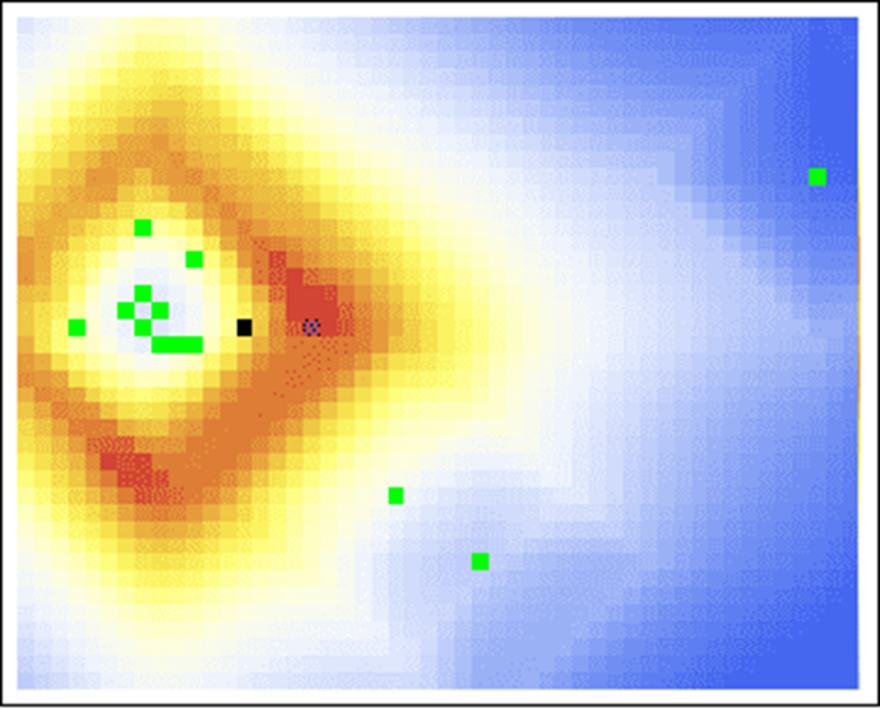
source: https://www.jeremykun.com/2011/07/20/serial-killers/
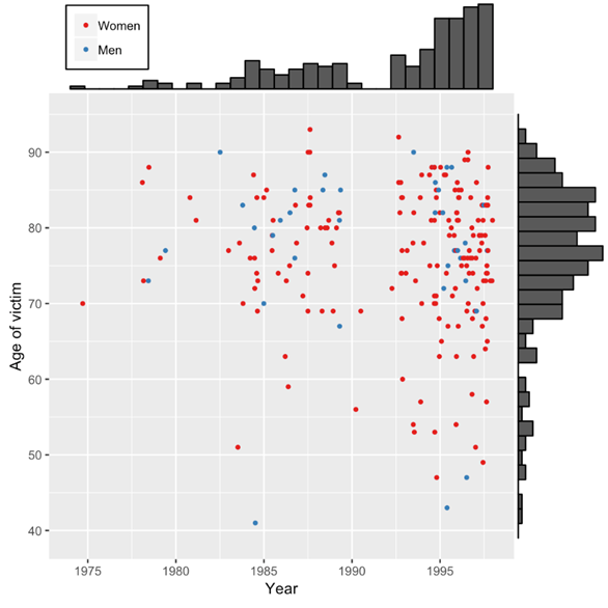
ภาพที่เห็นนี้เป็นข้อมูลจริงจากคดี The Boston Strangler ซึ่งเป็นคดีฆาตกรรมต่อเนื่องโดย อัลเบิร์ต เดซาลโว (Albert DeSalvo) เขาได้ฆาตกรรมผู้หญิง 13 คนระหว่างปี 1962-1964 โดยจุดสีเขียวในภาพแสดงตำแหน่งที่เกิดคดีของแต่ละคดี สีที่เห็นบนแผนที่นั้นคำนวณมาจาก Rossmo’s formula โดยมันจะแสดงความน่าจะเป็นที่ที่พักของคนร้ายจะอยู่ตรงนั้น สีแดงแปลว่ามีโอกาสสูง เหลืองคือต่ำลงมา และสีน้ำเงินคือคนร้ายไม่น่าจะอาศัยอยู่แถวนั้น
ซึ่งจากภาพจะเห็นว่ามีบริเวณพีคสีแดงเข้มอยู่สองจุด และเมื่อจับคนร้ายได้ ตำรวจพบว่าจุดเล็กๆ สีม่วงซึ่งแสดงถึงตำแหน่งที่พักของฆาตกรนั้นอยู่ในโซนแดงเข้มพอดี ตัวอย่างนี้เป็นการแสดงให้เห็นว่า Rossmo’s formula นั้นสามารถนำมาใช้ในการระบุตำแหน่งของคนร้ายได้อย่างแม่นยำ แต่นี่เป็นคดีที่เกิดขึ้นไปแล้วและได้ปิดคดีไปแล้ว ถ้า Rossmo’s formula นี้ดีจริงมันต้องช่วยเราจับคนร้ายที่ยังตามจับไม่ได้หรือช่วยสืบคดีที่ยังมีการสืบสวนอยู่สิ คำถามคือ Rossmo’s formula นี้ทำได้รึเปล่า
เริ่มจากคดีแรกซึ่งเป็นคดีฆ่าข่มขืน 5 ศพในประเทศอังกฤษในช่วงปี 1982-1995 เนื่องจากสถานที่ก่อเหตุของคดีนี้อยู่ในหลายเมือง จึงทำให้บริเวณที่น่าสงสัยกินพื้นที่มากกว่า 7000 ตารางกิโลเมตร และมีผู้ต้องสงสัยมากกว่า 12,000 คน ในปี1997 คิม รอสโมได้ถูกเรียกตัวเข้ามาช่วยเหลือคดีนี้ ภายใต้ชื่อ Operation Lynx และหลักฐานชิ้นสำคัญที่ช่วยให้คิมระบุตัวคนร้ายได้คือบัตรเครดิตที่อยู่ในรถที่คนร้ายขโมยมาใช้ก่อเหตุ
โดยคิม รอสโมพบว่ารายการใช้จ่ายของบัตรเครดิตที่ถูกขโมยมานี้ส่วนใหญ่มักซื้อของกินของใช้ทั่วไป เช่น เสื้อผ้า บุหรี่ เหล้า ซึ่งเป็นของที่คนเลือกซื้อในเส้นทางที่เดินทางเป็นประจำ คิมเลยใช้สมการของเขากับข้อมูลการใช้บัตรเครดิตซื้อของประกอบกับสถานที่ก่อเหตุของคนร้ายในการระบุตำแหน่งที่คนร้ายน่าจะอาศัยอยู่
จากการคำนวณพบว่าคนร้ายน่าจะอาศัยอยู่ในเขต Millgarth หรือ Killingbeck ซึ่งช่วยให้ตำรวจเร่งการสืบสวนในพื้นที่เหล่านี้จนจับตัวคนร้ายได้ในเดือนมีนาคม1998 โดยคนร้ายอาศัยอยู่ในเขต Killingbeck จริงตามที่สมการของเขาระบุไว้ แต่ที่น่าทึ่งกว่านั้นคือเขต Millgarth ซึ่งเป็นอีกหนึ่งเขตที่สมการรอสโมคาดการณ์ไว้นั้นเป็นเขตที่แม่ของคนร้ายอาศัยอยู่ และคนร้ายมักจะไปเยี่ยมแม่ของเขาหลายครั้ง
เท่ากับว่าสมการรอสโมนั้น
สามารถระบุที่พักของคนร้ายและสถานที่ที่คนร้ายมักจะไปได้อย่างแม่นยำมาก
คดีต่อมามีชื่อเรียกกันว่า Lafayette South Side Rapist เป็นคดีฆ่าข่มขืนที่เกิดขึ้นในเมือง Lafayette รัฐ Louisiana ที่เกิดขึ้นยาวนานกว่า 10 ปี ตั้งแต่ 1988-1998 และมีเหยื่อ 14 คน คุณ Rossmo ได้ถูกเรียกตัวมาช่วยสืบคดีนี้ร่วมกับ Vancouver Police Department (VPD)
ซึ่งในขณะนั้นตำรวจยังเชื่อว่าคดีนี้เป็นเพียงคดีคนสูญหายที่ไม่ได้มีความเกี่ยวข้องกัน แต่คุณรอสโมได้ทำการรวบรวมข้อมูลเกี่ยวกับรายงานคนหายที่เกิดขึ้นและพบว่าเหตุการณ์เหล่านี้มีความเชื่อมโยงกันและเป็นฝีมือของคนร้ายคนเดียวกัน สมการของเขาถูกใช้ระบุพื้นที่ที่คนร้ายน่าจะอาศัยอยู่ เมื่อประกอบกับหลักฐานอื่นๆ แล้ว ตำรวจได้จับกุมตัวคนร้ายได้สำเร็จและที่อยู่ของคนร้ายในช่วงที่เกิดเหตุก็ตรงกับผลการวิเคราะห์ด้วย Rossmo’s formula เป๊ะเลย
หลังจากปิดคดี Lafayette South Side Rapist ได้แล้ว คิม รอสโซก็ได้มาร่วมงานกับ VPD อีกครั้งในคดีของโรเบิร์ต พิคทัน (Robert Pickton) ซึ่งเป็นคดีฆาตกรรมต่อเนื่องผู้หญิงกว่า27 คน ในตอนแรกตำรวจทุกคนไม่มีใครคาดคิดว่าคดีที่เกิดขึ้นเหล่านี้มาจากผู้ก่อเหตุคนเดียวกัน แต่กลับกลายเป็นคิม รอสโมที่วิเคราะห์สถานที่เกิดเหตุต่างๆ ด้วยสมการของเขาและนำมาประกอบกับหลักฐานอื่นๆ จนตั้งข้อสันนิษฐานได้ว่าทั้งหมดนี้เป็นฝีมือของฆาตกรต่อเนื่องคนเดียวกันอย่างแน่นอน
แต่ว่าหลังจากนำเสนอรายงาน การวิเคราะห์ของคิม รอสโมกลับถูกปฏิเสธจากหัวหน้านักสืบของคดี และยังหยามว่าการวิเคราะห์ของคุณคิมนั้นเป็นเพียงทฤษฎีสมคบคิด ยิ่งไปกว่านั้น กรมตำรวจได้ลดยศของคุณคิมพร้อมกับไม่ต่อสัญญาจ้างของคุณคิมในปี 2000 ถึงแม้ว่ายังจะปิดคดีไม่ได้ก็ตาม
หลังจากนั้น Royal Canadian Mounted Police ก็ได้เข้ามาสืบคดีนี้ด้วยอีกแรง แต่กว่าจะจับกุมคนร้ายได้ก็ใช้เวลาถึง 2 ปีหลังจากที่ไล่คุณคิมออก แถมสุดท้ายแล้วคนร้ายที่จับได้นั้นก็เป็นฆาตกรต่อเนื่องตามที่คุณคิมตั้งข้อสันนิษฐานไว้ตั้งแต่แรกด้วย
ทำให้ในปี 2010 ได้เกิดการสอบสวนเกี่ยวกับบทบาทหน้าที่ของ Vancouver Policde Department และ Royal Canadian Mounted Police ในคดีโรเบิร์ต พิคทัน ซึ่งคุณคิมก็ได้มาเป็นพยานให้ด้วย ตอนนั้นเขาพูดว่าสิ่งที่เกิดขึ้นในคดีนี้เปรียบได้กับการที่สถานีดับเพลิงไม่ส่งรถดับเพลิงไปเพราะว่าไม่เห็นไฟถึงแม้ว่าจะเห็นควันอยู่ตรงหน้าก็ตาม ถ้าหากในตอนนั้นตำรวจเชื่อสิ่งที่คุณคิมรายงาน คนร้ายก็อาจจะไม่ลอยนวลมานานขนาดนี้
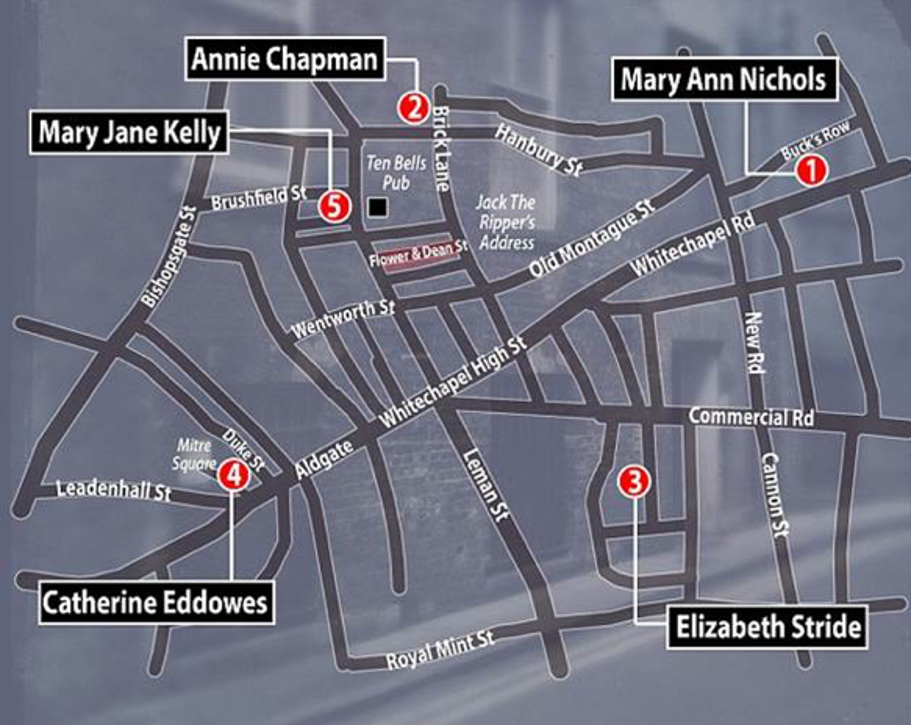
source: https://tomrocksmaths.com/2018/12/06/not-so-smooth-criminals-how-to-use-maths-to-catch-a-serial-killer/
ด้วยความโด่งดังของเทคนิคการทำ Geospatial Profiling จึงทำให้ในปี 2018 ทอม ครอว์ฟอร์ด (Tom Crawford) อาจารย์ภาควิชาคณิตศาสตร์ที่มหาวิทยาลัยอ็อกซ์ฟอร์ดได้นำเทคนิคนี้มาลองใช้กับข้อมูลจากคดี Jack the Ripper ที่แสนโด่งดัง ว่าเราสามารถจำกัดตำแหน่งของฆาตกรคนนี้ได้หรือไม่จากสถานที่ฆาตกรรมที่เกิดขึ้นในบล็อกของเขา ผลจากการทำ Geospatial Profiling โดยใช้ข้อมูลคดีฆาตกรรมทั้ง 5 ทั้งแสดงให้เห็นว่า Jack the Ripper นั้นน่าจะอาศัยอยู่ที่ถนน Flower & Deane ซึ่งก็ไม่มีใครบอกได้ว่าเป็นอย่างนั้นจริงๆ หรือไม่
จะเห็นได้ว่าคณิตศาสตร์ก็มีบทบาทสำคัญในการไขคดีฆาตกรรมไม่แพ้วิทยาศาสตร์ ถึงแม้ในความเป็นจริงมนุษย์ไม่ได้ทำทุกอย่างมีแบบแผนเป๊ะๆ ไปไปเสียหมด แต่จากคดีที่เล่ามาก็น่าจะพอทำให้เห็นว่า เมื่อเราสามารถใช้คณิตศาสตร์ในการสกัดรูปแบบหรือแก่นของสิ่งที่ดูยุ่งเหยิงออกมาให้ตีความได้สะดวกมากขึ้น และต่อให้คุณไม่เชื่อในพลังของคณิตศาสตร์เหมือนกับคุณหัวหน้านักสืบท่านนั้น สุดท้ายพลังของคณิตศาสตร์ก็จะปรากฏให้คุณเห็นเอง
อ้างอิงจาก
assets.publishing.service.gov.uk